ארכימדס ביוגרפיה, תרומות והמצאות

ארכימדס מסירקיוז (287 a.C - 212 a.C) היה מתמטיקאי, פיסיקאי, ממציא, מהנדס ואסטרונום יווני מהעיר העתיקה סירקיוז, באי סיציליה. התרומות הבולטות ביותר שלו הן העיקרון של ארכימדס, פיתוח שיטת exhaution, השיטה מכני או את היצירה של הפלנטריום הראשון.

כרגע זה נחשב כמו אחד משלושת הדמויות החשובות יותר של המתמטיקה של עתיקות ליד Euclides ו Apolonio, שכן התרומות שלה פירושו התקדמות מדעית חשובה עבור הזמן בתחומים של חישוב, פיזיקה, גיאומטריה אסטרונומיה. בתורו, זה הופך אותו לאחד המדענים הבולטים בהיסטוריה של האנושות. 

אף כי פרטים מעטים על חייו האישיים ידועים - ואלה הידועים באמינות מפוקפקת - תרומתו ידועה הודות לסדרת מכתבים כתובים על יצירותיו והישגיו, שנשמרו עד ימינו, אל התכתובת שהוא שמר במשך שנים עם חברים ועם מתמטיקאים אחרים של אותה תקופה.

ארכימדס היה מפורסם בזמנו בזכות ההמצאות שלו, אשר משכה את תשומת הלב של בני דורו, בין השאר משום שהם שימשו כמכשיר מלחמה כדי למנוע בהצלחה פלישות רומאיות רבות..

עם זאת, הוא אמר כי הוא טען כי הדבר היחיד באמת היה חשוב במתמטיקה, וכי המצאותיו היו רק תוצר של הבילוי של גיאומטריה יישומית. בדורות הבאים, יצירותיו במתמטיקה טהורה הוערכו הרבה יותר מהמצאותיו.

אינדקס

• 1 ביוגרפיה
  • 1.1 הדרכה
  • 1.2 עבודה מדעית
  • 1.3 סכסוך בסירקיוז
  • 1.4 מוות
• 2 תרומות מדעיות של ארכימדס
  • 2.1 עקרון ארכימדס
  • 2.2 שיטה מכנית
  • 2.3 הסבר על חוק המנוף
  • 2.4 פיתוח שיטת ה - Exhution או דלדול ההפגנה המדעית
  • 2.5 מדד המעגל
  • 2.6 הגיאומטריה של כדורים וצילינדרים
• 3 המצאות
  • 3.1 מד מרחק
  • 3.2 הפלנטריום הראשון
  • 3.3 בורג ארכימדס
  • 3.4 הטופר של ארכימדס
• 4 הפניות

ביוגרפיה

ארכימדס של סירקיוז נולד בערך בשנת 287 לפנה"ס. לא ידוע הרבה על שנותיו הראשונות, אם כי אפשר לומר שהוא נולד בעיר סירקיוז, עיר שנחשבה לנמל הראשי של האי סיציליה, היום באיטליה..

באותו זמן, סירקיוז היה אחד הערים שהרכיבו את מה שמכונה מגנא גרסיה, אשר היה שטח מיושב על ידי מתנחלים ממוצא יווני לאזור הדרומי של חצי האי של איטליה בסיציליה.

אין עובדות ידועות על אמו של ארכימדס. ביחס לאב, ידוע כי זה נקרא Phidias וכי הוא היה מוקדש אסטרונומיה. מידע זה של אביו ידוע בזכות קטע של הספר דלפק החול, שנכתב על ידי ארכימדס, שבו הוא מזכיר את שמו של אביו.

הרקלידס, שהיה פילוסוף ואסטרונום יווני, חיבב מאוד את ארכימדס ואף כתב עליו ביוגרפיה. עם זאת, המסמך לא נשמר, ולכן כל המידע הכלול בו אינו ידוע.

מאידך גיסא, ההיסטוריון, הפילוסוף והביוגרף פלוטארקו ציין בספרו "חיים מקבילים" שארכימדס קיים קשר דם עם היורו השני, עריץ שהיה ממונה בסירקיוז מאז 265 לפנה"ס.

הדרכה

כתוצאה ממידע קטן שיש לנו על ארכימדס, אנחנו לא יודעים בוודאות היכן הוא השיג את האימון הראשון שלו.

עם זאת, היסטוריונים שונים קבעו כי קיימת אפשרות גבוהה כי ארכימדס למד באלכסנדריה, שהיה מרכז התרבות היוונית וההוראה החשוב ביותר באזור..

הנחה זו נתמכת על ידי המידע שהוצע על ידי ההיסטוריון היווני דיודורו סיקולו, שציין כי ארכימדס למד כנראה באלכסנדריה.

יתר על כן, ברבים מיצירותיו ארכימדס עצמו מזכיר מדענים אחרים של הזמן שעבודתם מתמקדת באלכסנדריה, כך שאתה יכול להניח למעשה כי פרשת בעיר הזאת.

חלק מהאישים שאריצ'מדס האמין כי הם פעלו באלכסנדריה הם הגיאוגרף, המתמטיקאי והאסטרונום ארטוסטנס של סיירין, והמתמטיקאי והאסטרונום קונון דה סנוס.

מוטיבציה משפחתית

מאידך גיסא, העובדה שאביו של ארכימדס היה אסטרונום, אולי השפיעה במידה ניכרת על נטיותיו שהראה לאחר מכן, כי בהמשך ובגיל צעיר היתה משיכה מיוחדת בתחום מדעים.

לאחר זמנו באלכסנדריה, ההערכה היא כי ארכימדס חזר סירקיוז.

עבודה מדעית

לאחר שחזר סירקיוז, ארכימדס החלו להמציא חפצים שונים אשר בקרוב זכה לו פופולריות מסוימת בקרב תושבי העיר הזאת. בתקופה זו הוא נתן את עצמו לחלוטין לעבודות מדעיות, הפיק המצאות שונות והסיק כמה מושגים מתמטיים מתקדמים מאוד לזמנו.

לדוגמה, כאשר הוא הקדיש את עצמו ללמוד את המאפיינים של דמויות מעוקל שטוח שטוח, הוא בא עם מושגים הקשורים אינטגרלי חשבון אינטגרלי, אשר פותחה מאוחר יותר.

כמו כן, ארכימדס היה זה שהגדיר כי נפח הקשורים כדור מתאים פעמיים בגודל של הצילינדר המכיל אותו, והוא היה מי המציא את הגלגלת מרוכבים, על סמך תגליותיו על החוק של המנוף.

קונפליקט בסירקיוז

בשנת 213 לפנה"ס נכנסו חיילים רומיים לעיר סירקיוז והקיפו את מתנחליה על מנת לגרום להם להיכנע.

פעולה זו הובלה על ידי הצבא והמדינאי היווני מרקו קלאודיו מרסלו במסגרת המלחמה הפונית השנייה. מאוחר יותר, זה היה ידוע בתור חרב רומא, שכן זה בסופו של דבר לכבוש סירקיוז.

באמצע הסכסוך, שנמשך שנתיים, נלחמו תושבי סירקיוז ברומאים באומץ ובפראות, וארכימדס מילא תפקיד חשוב מאוד, שכן הוא הקדיש את עצמו ליצירת כלים ומכשירים שעזרו להביס את הרומאים.

לבסוף, לקח מרקו קלאודיו מרסלו את העיר סירקיוז. לפני האינטלקטואליות הגדולה של ארכימדס, הורה מרסלו שלא ייפגעו ולא ייהרגו. עם זאת, ארכימדס נהרג בידיו של חייל רומי.

מוות

ארכימדס מת בשנת 212 לפנה"ס. יותר מ -130 שנה לאחר מותו, בשנת 137 לפני הספירה, הסופר, הפוליטיקאי והפילוסוף מרקו טוליו קיקרו כבש תפקיד בממשל של רומא ורצה למצוא את קברו של ארכימדס.

משימה זו לא היתה קלה, שכן Cicero לא יכול למצוא מישהו כדי לציין את המקום המדויק. עם זאת, בסופו של דבר הוא הגיע, קרוב מאוד לדלת של Agrigento בתנאים מצער.

Cicero ניקה את הקבר וגילה כי הוא היה כתוב עם כדור בתוך גליל, כמו התייחסות לגילוי על נפח כי ארכימדס עשה לפני כמה זמן..

גרסאות על מותו

הגרסה הראשונה

אחת הגרסאות קובע כי ארכימדס היה באמצע של פתרון בעיה מתמטית כאשר הוא ניגש על ידי חייל רומי. אומרים שארכימדס יכול היה לבקש ממנו זמן מה לפתור את הבעיה, כך שהחייל היה הורג אותו.

גרסה שנייה

הגרסה השנייה דומה הראשונה. חשבון ארכימדס היה לפתור בעיה של מתמטיקה כאשר לוקחים את העיר התרחשה.

חייל רומאי נכנס למתחם שלו והורה לו לפגוש מרסלו, שבו ארכימדס השיב כי לפני בפתרון הבעיה שעליה הוא עובד. החייל התרגז בעקבות תגובה זו והרג אותו.

גרסה שלישית

השערה זו מעידה כי ארכימדס היה בידיו מגוון רחב של כלים אופייניים למתמטיקה. ואז, חייל ראה אותו והוא חשב שהוא עלול לשאת חפצים יקרי ערך, אז הוא הרג אותו.

גרסה רביעית

גרסה זו ממחישה כי ארכימדס כרע ליד הקרקע, שוקל תוכניות שהוא לומד. ככל הנראה, חייל רומי בא מאחור, לא מודע לכך היה ארכימדס, ירה בו.

תרומות מדעיות של ארכימדס

העיקרון של ארכימדס

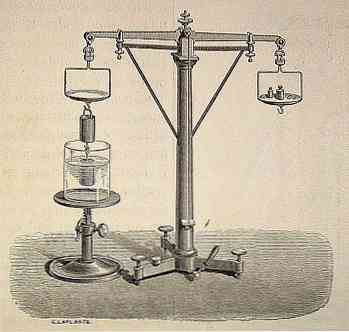
העיקרון של ארכימדס נחשב על ידי המדע המודרני כאחד המורשת החשובה ביותר של התקופה העתיקה.

לאורך ההיסטוריה, בעל פה, דווח כי ארכימדס הגיע לגילוי שלו בטעות בזכות המלך הירון הזמין לראות אם כתר זהב, שנשלח לייצר על ידו, נעשה רק זהב טהור ולא הכיל שום מתכת אחרת. הייתי צריך לבצע את זה בלי להרוס את הכתר.

ארכימדס הוא אמר כי בעוד מהרהר איך לפתור את הבעיה הזו החליטה לעשות אמבטיה ולהיכנס לאמבט הבין כי מפלס המים גדל כשהוא טובל בכל זאת.

בדרך זו, הוא יגלה את העיקרון המדעי כי "כל גוף שקוע כולו או בחלקו בנוזלים (נוזלים או גז) מקבל דחיפה כלפי מעלה, השווה למשקל הנוזל שמוזר על ידי האובייקט".

עיקרון זה אומר שהנוזלים מפעילים כוח עולה - דוחפים כלפי מעלה - על כל חפץ שקוע בהם, וכי כמות כוח הדחיפה הזה שווה למשקל הנוזל הנעדר על ידי הגוף השקוע, ללא קשר למשקלו.

ההסבר לעיקרון זה מתאר את תופעת ההנפקה, ונמצא בה אמנה על גופים צפים.

עיקרון ארכימדס יושם מאוד עבור אובייקטים צפים הדורות לשימוש המוני כמו צוללות, ספינות, חגורות הצלה ובלונים.

שיטה מכנית

עוד התרומות החשובות ביותר ארכימדס המדע היה הכללת שיטה מכנית גרידא ההיא." לומר, חשיבה טכנית להנמקה של בעיות גיאומטריות, ופירוש באופן חסר תקדים כדי לפתור את הבעיות הללו בפעם.

בהקשר של ארכימדס, הגיאומטריה נחשבה למדע תיאורטי בלבד, והדבר הנפוץ היה שהמתמטיקה הטהורה ירדה אל מדעים מעשיים אחרים, שבהם ניתן ליישם את עקרונותיה..

מסיבה זו, כיום היא נחשבת כמקדמת המכניקה כמשמעת מדעית.

בכתב שבו המתמטיקאי חושף את השיטה החדשה לחברו ארטוסטנס, מציין כי זה מאפשר לטפל בבעיות במתמטיקה באמצעות מכניקה, וכי זה קצת יותר קל לבנות את ההפגנה של משפט גיאומטרי אם זה כבר יש כמה ידע מעשי קודם, כי אם אין לך מושג על זה.

שיטה חדשה זו של החקירה שתבוצע על ידי ארכימדס תהפוך לבשר של השלב הלא פורמלי של גילוי וניסוח ההשערה של השיטה המדעית המודרנית.

הסבר על חוק המנוף

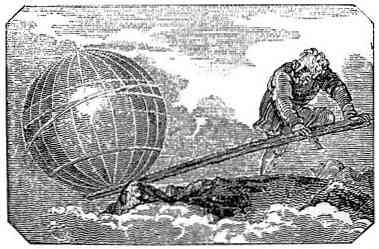
בעוד מנוף הוא מכונה פשוטה אשר שימש מאז הרבה יותר מוקדם ארכימדס, זה היה הוא אשר ניסח את העיקרון המסביר את פעולתו מסה שלו על מאזן המטוסים.

בניסוחו של חוק זה, ארכימדס קובע עקרונות המתארים את ההתנהגות של מנוף שונה כאשר הנחת שני גופים על זה, בהתאם למשקל שלה ואת המרחק שלה מנקודת תמיכה.

בדרך זו הוא מצביע על כך ששני גופים המסוגלים להיות נמדדים (ניתנים למדידה), הממוקמים על מנוף, מאוזנים כאשר הם נמצאים במרחקים הפוך ביחס למשקלם.

באותו אופן, גופים בלתי ניתנים למדידה (אשר לא ניתן למדוד) לעשות זאת, אבל החוק הזה היה הוכח על ידי ארכימדס רק עם גופים מהסוג הראשון.

ניסוחו של עקרון המנוף הוא דוגמה טובה ליישום השיטה המכנית, שכן על פי ההסבר במכתב המופנה אל Dositeo, זה התגלה ברגע הראשון בשיטות של המכניקה שהניבו הלכה למעשה.

מאוחר יותר הוא ניסח אותם באמצעות שיטות של גיאומטריה (תיאורטית). מן הניסוי הזה על הגופים גם את הרעיון של מרכז הכובד היה מנותק.

פיתוח שיטת ההתראה או התשישות של ההפגנה המדעית

תשישות היא שיטה המשמשת בגיאומטריה המורכבת מקירוב של נתונים גיאומטריים ששטחם ידוע, באמצעות הכיתוב והעיגול, על שטח אחר שאזורו אמור להיות ידוע..

למרות ארכימדס לא היה יוצר של שיטה זו, הוא פיתח אותו masterfully, והצליח לחשב באמצעות אותו ערך מדויק של Pi.

ארכימדס, תוך שימוש בשיטת ההזהרה, במשיכות ובמשושים המוגדרים להיקף של קוטר 1, בהקטנת האבסורד ההבדל בין שטח המשושים לבין היקף ההיקף.

כדי לעשות זאת, הוא חצה את משושים ליצור פוליגונים של עד 16 הצדדים, כפי שמוצג בתרשים הקודם.

בדרך זו, הוא בא לציין כי הערך של pi (של הקשר בין אורך המעגל ואת קוטר) הוא בין הערכים 3.14084507 ... ו 3.14285714 ... .

ארכימדס נהגה להשתמש בשיטת exhaución כי לא רק הצליח לחשב את החישוב של הערך של פי עם מרווח של טעות נמוך למדי, ולכן הרצוי, אלא גם, כי פי הוא מספר לא רציונלי, דרך שיטה זו והתוצאות שהושגו הניחו את היסודות שייווצרו במערכת החישוב האינסופית, ומאוחר יותר,.

מדד המעגל

כדי לקבוע את שטח המעגל, ארכימדס השתמש בשיטה שכללה ציור ריבוע שמתאים בדיוק בתוך מעגל. 

בידיעה כי שטח הריבוע הוא הסכום של הצדדים שלה, כי שטח המעגל היה גדול יותר, הוא החל לעבוד על קבלת קירובים. זה עשה על ידי החלפת הכיכר עם מצולע 6 צדדית ולאחר מכן עובד עם מצולעים מורכבים יותר.

ארכימדס היה המתמטיקאי הראשון בהיסטוריה להתקרב ביצוע חישוב רציני של מספר Pi.

הגיאומטריה של כדורים וצילינדרים

בין תשעת מסות קומפילציה את העבודה של ארכימדס במתמטיקה ובפיסיקה, ישנם שני כרכים על הגיאומטריה של כדורים וצילינדרים.

עבודה זו עוסקת בקביעה כי פני השטח של כל תחום רדיוס הוא פי ארבעה מזה של המעגל הגדול ביותר שלו, וכי נפח כדור הוא שני שלישים כי של הצילינדר שבו הוא חרוט.

המצאות

מד מרחק

ידוע גם בשם קילומטרים, זה היה המצאה של האיש המפורסם הזה.

התקן זה נבנה על פי העיקרון של גלגל, כאשר הוא מסתובב, מפעיל הילוכים המאפשרים לחשב את המרחק נסע..

על פי אותו עיקרון, ארכימדס תכנן מספר סוגים של מדחומים למטרות צבאיות ואזרחיות.

הפלנטריום הראשון

בהתבסס על עדותו של סופרים קלאסיים רבים כמו קיקרו, אובידיוס, Claudian, מרציאנו Capela, Casiodoro, סקסטוס אמפיריקוס ו Lactancio, היום מדענים רבים מייחסים ארכימדס בריאת פלנטרית בסיסי הראשון.

זהו מנגנון היוצר סדרה של "ספירות" שהצליחו לחקות את תנועת כוכבי הלכת. עד כה הפרטים של מנגנון זה אינם ידועים.

לפי קיקרו, הפלנטריום שנבנה על ידי ארכימדס היה שני. באחת מהן הוצגו הקרקע והמערכות השונות שלצדה.

בשנייה, עם סיבוב אחד, השמש, הירח וכוכבי הלכת עשו את התנועות העצמאיות שלהם ביחס לכוכבים הקבועים, בדיוק כפי שעשו ביום אמיתי. בחודש האחרון, בנוסף, ניתן לצפות בשלבים רצופים ליקויי הירח.

הבורג של ארכימדס

הבורג ארכימדס הוא מכשיר המשמש להובלת מים מלמטה למעלה דרך מדרון, באמצעות צינור או צילינדר.

לדברי ההיסטוריון היווני דיודורו, הודות להמצאה זו הוא הקל על השקיה של אדמות פורייה הממוקמות לאורך נהר הנילוס במצרים הקדומה, שכן הכלים המסורתיים דרשו מאמץ פיזי עצום שמיצה את העובדים.

גליל בשימוש יש בתוך בורג של אורך זהה, אשר שומרת מחוברים מערכת של מדחפים או סנפירים המבצעים תנועה סיבוב מונע באופן ידני על ידי מנוף מסתובב.

בדרך זו, הצלחות מצליחות לדחוף כל חומר מלמטה למעלה, ויוצרות מעין מעגל אינסופי.

הציפורן של ארכימדס

הציפורן של ארכימדס, או יד הברזל כפי שהיא ידועה, היתה אחד מכלי הנשק המפחידים ביותר שנוצרו על ידי המתמטיקאי הזה, והפך להיות החשוב ביותר להגנה הסיציליאנית על הפלישות הרומיות.

על פי מחקר שנערך על ידי פרופ 'Drexel פרופסורים כריס Rorres (המחלקה למתמטיקה) והארי האריס (המחלקה להנדסה אזרחית ואדריכלות), זה היה מנוף גדול כי היה וו לתפוס מחובר למנוף באמצעות שרשרת שנתלתה ממנה.

באמצעות המנוף, כך הקרס נפל על ספינת האויב עבר מניפולציה, ואת המטרה הייתה לחבר אותו ולהעלות אותו במידה כזו כי שחרורו הושג לחלוטין לבטל או לגרום לו לקרוס אל סלעי החוף.

Rorres והאריס שהוצגו בסימפוזיון "מכונות ומבנים יוצאי דופן של העת העתיקה" (2001), ייצוג מיניאטורי של המכשיר הזה תחת הכותרת "מכונת מלחמה אדירה: הקמה ותפעול של יד ברזל של ארכימדס"

למימוש עבודה זו הם הסתמכו על טיעוני ההיסטוריונים הקדומים פוליביו, פלוטארקו וטיטו ליביו.

הפניות

1. Assis, A. (2008). ארכימדס, מרכז הכובד, והחוק הראשון של מכניקה [באינטרנט]. גישה 10 יוני 2017 על bourabai.ru.
2. דייקסטרהויז, 1956. ארכימדס [מקוון]. הגישה ל -9 ביוני 2015 ב- World Wide Web: books.google.co.ve/books.
3. MOLINA, A. (2008). שיטת המחקר של ארכימדס של סירקיוז: אינטואיציה, מכניקה ו exhaution [באינטרנט]. גישה ב -10 ביוני 2017 ב World Wide Webproduccioncientifica.luz.edu.
4. או'קונור, י 'ורוברסון, ר' (1999). ארכימדס של סירקיוז [באינטרנט]. גישה 9 יוני 2017 בשעה history.mcs.st-and.ac.uk.
5. PARRA, E. (2009). ארכימדס: חייו, יצירותיו ותרומותיו למתמטיקה המודרנית [באינטרנט]. אחזור ב -9 ביוני 2017 ב lfunes.uniandes.edu.co.
6. QUINN, L. (2005). ארכימדס של סירקיוז [באינטרנט]. גישה 9 יוני, 2017 ב math.ucdenver.edu.
7. RORRES, C. & HARRIS, H. (2001). מכונת מלחמה אדירה: בנייה ותפעול של יד ברזל של ארכימדס [באינטרנט]. אחזור ב -10 ביוני 2017 ב cs.drexel.edu.
8. VITE, L. (2014). עקרון ארכימדס [באינטרנט]. אחזור ב -10 ביוני 2017 ב repository.uaeh.edu.mx.