מערכת קוליניארית ודוגמאות

ה וקטורים קוליניריים הם אחד משלושת סוגי הווקטורים הקיימים. זה על אלה וקטורים כי הם באותו כיוון או קו פעולה. פירוש הדבר: שני או יותר וקטורים יהיו קולינירים אם הם מסודרים בקווים ישרים מקבילים זה לזה.

וקטור מוגדר ככמות המוחלת על גוף ומאופיין כבעל כיוון, חוש ומידה. את הווקטורים ניתן למצוא במישור או בחלל והוא יכול להיות מסוגים שונים: וקטורים קוליניריים, וקטורים בו זמנית וקטורים מקבילים.

אינדקס

• 1 וקטורים קולינליים
• 2 מאפיינים
  • 2.1 דוגמה 1
  • 2.2 דוגמה 2
  • 2.3 דוגמה 1
• 3 מערכת וקטור קוליניארית
  • 3.1 וקטורים קוליניריים עם חושים הפוכים
  • 3.2 וקטורים קוליניאריים עם אותה תחושה
  • 3.3 וקטורים קוליניאריים בעלי גודל שווה וחושים הפוכים
• 4 ההפרש בין וקטורים קולינריים ווקטוריים
• 5 הפניות

וקטורים קוליניאריים

וקטורים הם קוליניאריות אם קו הפעולה של אחד הוא בדיוק אותו קו פעולה של כל וקטורים אחרים, ללא קשר לגודל ותחושה של כל אחד וקטורים.

ווקטורים משמשים לייצוגים בתחומים שונים כגון מתמטיקה, פיזיקה, אלגברה וגם בגיאומטריה, כאשר וקטורים הם קוליניאריים רק כאשר הכיוון שלהם זהה, ללא קשר למשמעות שלהם.

תכונות

- שניים או יותר הם וקטורים collinear אם היחסים בין הקואורדינטות שווה.

דוגמה 1

יש לנו את הווקטורים m = m_x; m_y ו- n = n_x; n_y. אלה הם קוליניאריים אם:

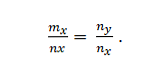
דוגמה 2

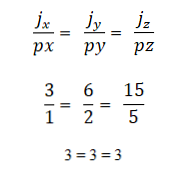
- שני וקטורים או יותר הם קוליניאריים אם הכפל של המוצר או הווקטור שווה לאפס (0). הסיבה לכך היא שבמערכת הקואורדינטות, כל וקטור מאופיין בקואורדינטות המתאימות לו, ואם אלה הם פרופורציונליים זה לזה, הווקטורים יהיו קולינאריים. זה בא לידי ביטוי כדלקמן:

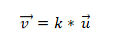
דוגמה 1

יש לנו את הווקטורים = (10, 5) ו- b = (6, 3). כדי לקבוע אם הם קוליניאריים התיאוריה הקובע מוחל, אשר קובע את השוויון של מוצרים לחצות. בדרך זו, עליך:

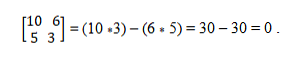
מערכת וקטור קוליניארית

וקטורים קולינירים מיוצגים בצורה גרפית באמצעות כיוון ותחושה של אלה - בהתחשב בכך שהם חייבים לעבור דרך נקודת היישום - ואת המודול, אשר הוא קנה מידה מסוים או אורך.

מערכת של וקטורים קוליניאריים נוצר כאשר שני וקטורים או יותר לפעול על אובייקט או גוף, המייצג כוח ופועלים באותו כיוון.

לדוגמה, אם שני כוחות קוליניאריים מוחלים על גוף, התוצאה של אלה תלויה רק ​​בכיוון שבו הם פועלים. ישנם שלושה מקרים, שהם:

וקטורים קוליניריים עם חושים הפוכים

התוצאה של שני וקטורים קוליניאריים שווה לסכום של אלה:

R = Σ F = F₁ + F_2.

דוגמה

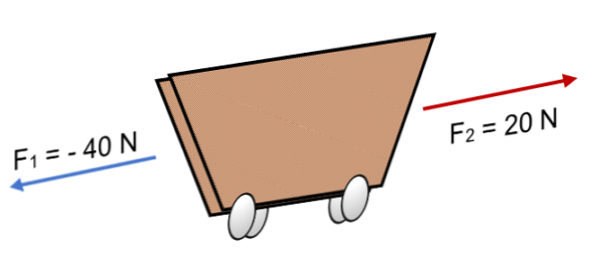
אם שני כוחות פועלים על עגלה F₁ = 40 N ו- F₂ 20 = N בכיוון ההפוך (כפי שמוצג בתמונה), התוצאה היא:

R = Σ F = (- 40 N) + 20N.

R = - 20 N.

קולינארית וקטורים עם אותה תחושה

גודל הכוח המתקבל יהיה שווה לסכום של וקטורים קוליניאריים:

R = Σ F = F₁ + F_2.

דוגמה

אם שני כוחות פועלים על עגלה F₁ 35 = N ו F₂ = 55 N באותו כיוון (כפי שמוצג בתמונה), התוצאה היא:

R = Σ F = 35 N + 55N.

R = 90 N.

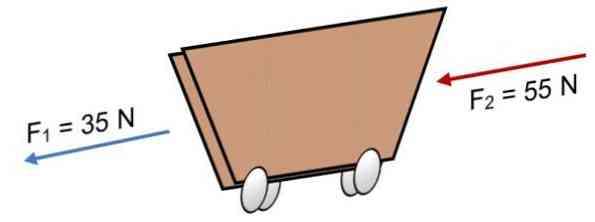
תוצאה חיובית עולה כי וקטורים קוליניאריים לפעול כלפי שמאל.

וקטורים קוליניאריים בעלי גודל שווה וחושים הפוכים

התוצאה של שני וקטורים קוליניאריים יהיה שווה לסכום של וקטורים קוליניאריים:

R = Σ F = F₁ + F_2.

מכיוון שלכוחות יש אותו גודל אבל בכיוון ההפוך - כלומר, אחד יהיה חיובי והשני שלילי - כאשר הוספת שני הכוחות תהיה התוצאה שווה לאפס.

דוגמה

אם שני כוחות פועלים על עגלה F₁ -7 -7 N ו- F₂ = 7 N, שיש להם אותו גודל אבל בכיוון ההפוך (כפי שמוצג בתמונה), התוצאה היא:

R = Σ F = (-7 N) + 7N.

R = 0.

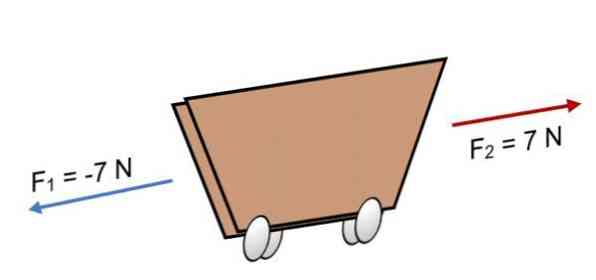
מכיוון שהתוצאה שווה ל -0, משמעות הדבר היא שהווקטורים מאוזנים זה כנגד זה, ולכן הגוף נמצא בשיווי משקל או במנוחה (הוא לא יזוז).

הבדל בין וקטורים קולינריים ווקטוריים

וקטורים קוליניאריים מאופיינים על ידי אותו כיוון באותו קו, או בגלל שהם מקבילים לקו; כלומר, הם וקווים מקבילים ישירות.

מצד שני, הווקטורים המקבילים מוגדרים משום שהם נמצאים בקווים שונים של פעולה אשר יירוט בנקודה אחת.

במילים אחרות, יש להם נקודת מוצא או הגעה - ללא תלות במודול, בכיוון או בכיוון שלהם - יוצרים זווית ביניהם.

המערכות של וקטורים מקבילים נפתרות על ידי שיטות מתמטיות או גרפים, שהם השיטה של ​​מקבילית הכוחות ואת שיטת המצולע של הכוחות. באמצעות אלה יקבע הערך של וקטור שהתקבל, אשר מציין את הכיוון שבו הגוף יעבור.

ביסודו של דבר, ההבדל העיקרי בין וקטורים קולינירים לבין וקטורים בו זמנית הוא קו הפעולה שבו הם פועלים: קוליניאריים לפעול באותו קו, ואילו אלה מקבילים שונים.

כלומר, וקטורים קוליניאריים לפעול במישור אחד, "X" או "Y"; ואת הפעולה במקביל בשני המטוסים, החל מאותה נקודה.

ווקטורים קוליניאריים אינם נמצאים בנקודה, כמו גם את אלה במקביל, כי הם מקבילים זה לזה.

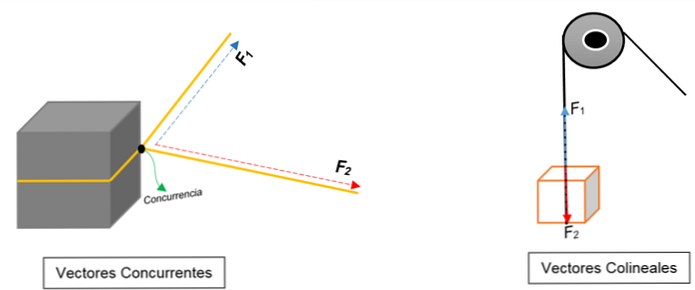
בתמונה השמאלית ניתן לראות בלוק. הוא קשור בחבל והקשר מחלק אותו לשניים; כאשר הוא נמשך לכיוון הכיוונים שונים עם כוחות שונים, הבלוק ינוע לכיוון באותו כיוון.

שני וקטורים מיוצגים כי מסכימים בנקודה (הבלוק), ללא קשר למודול שלהם, חוש או כיוון.

במקום זאת, בתמונה הנכונה מופיע גלגלת שמרימה קופסה. החבל מייצג את קו הפעולה; כאשר הוא מושך, שני כוחות (וקטורים) לפעול על זה: כוח אחד של מתח (כאשר מטפסים על בלוק) ועוד כוח, זה מפעיל את המשקל של הבלוק. לשניהם יש אותו כיוון אבל בכיוונים מנוגדים; לא מסכימים בנקודה.

הפניות

1. Estalella, J. J. (1988). ניתוח וקטור. כרך 1.
2. גופטא, א '(s.f.). טאטא מקגרו היל חינוך.
3. Jin Ho Kwak, S. H. (2015). אלגברה ליניארית. ספרינגר מדע ומדיה עסקית.
4. Montiel, H. P. (2000). הפקולטה לפיסיקה טכנולוגית. קבוצת העריכה של פטריה.
5. סנטיאגו בורבאנו דה ארסילה, ג '(2003). פיזיקה כללית עריכה טבר.
6. סינה, ק '(s.f.). ספר טקסט של המתמטיקה XII כרך 2. פרסומים Rastogi.