כמה צירים של סימטריה יש מעגל?

ה צירי סימטריה של מעגל הם אינסופיים. צירים אלה הם אלה המחלקים צורה גיאומטרית לשני חלקים שווים בדיוק.

ומעגל מורכב מכל הנקודות שהמרחק שלהן לנקודה קבועה קטן או שווה לערך מסוים "r".

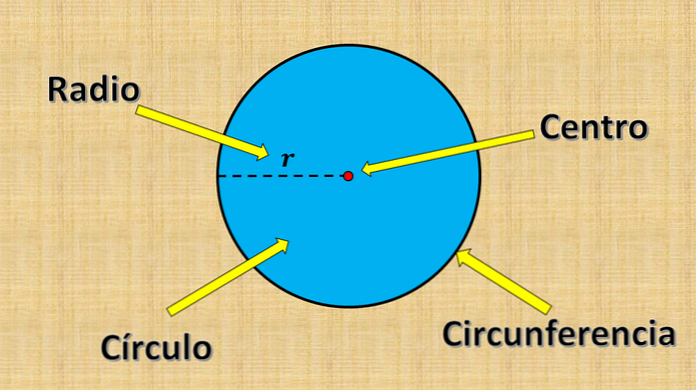
הנקודה הקבועה לעיל נקראת מרכז, והערך "r" נקרא רדיוס. הרדיוס הוא המרחק הגדול ביותר שיכול להיות בין נקודה על המעגל והמרכז.

מצד שני, כל קטע קטע אשר הקצוות נמצאים בקצה המעגל (היקף) ועובר במרכז נקרא קוטר. המדידה שלו תמיד שווה לרדיוס פעמיים.

מעגל והיקף

אל תבלבל מעגל עם מעגל. ההיקף מתייחס רק לנקודות הנמצאות במרחק של "ר" מהמרכז; כלומר, רק את קצה המעגל.

עם זאת, כאשר מחפשים את הצירים של סימטריה הוא אדיש אם אתה עובד עם מעגל או עם מעגל.

מהו ציר הסימטריה?

ציר הסימטריה הוא קו המחלק לשני חלקים שווים דמות גיאומטרית מסוימת. במילים אחרות, ציר הסימטריה פועל כמראה.

גלים של סימטריה של מעגל

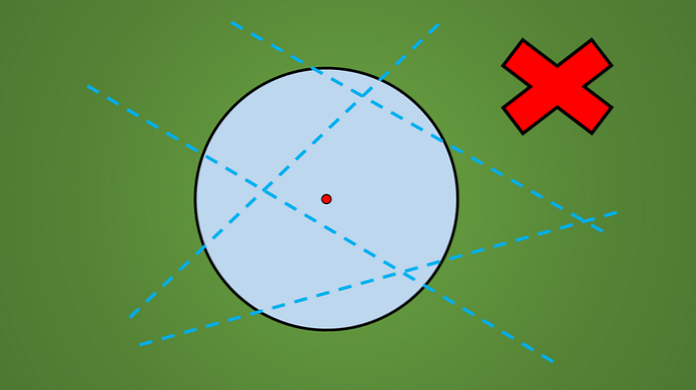
אם אתה מבחין במעגל כלשהו, ​​ללא קשר לרדיוס שלו, אתה יכול לראות שלא כל קו שחוצה אותו הוא ציר של סימטריה.

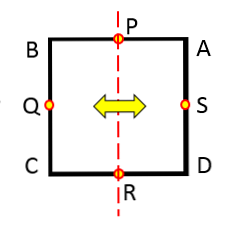
לדוגמה, אף אחד מהקווים המצוירים בתמונה הבאה הוא ציר הסימטריה.

דרך קלה לבדוק אם קו הוא ציר של סימטריה או לא, היא לשקף בצורה נייחת את הדמות הגיאומטרית אל הצד הנגדי של הקו.

אם ההשתקפות אינה מתאימה לדמות המקורית, אז הקו הזה אינו ציר של סימטריה. התמונה הבאה ממחישה טכניקה זו.

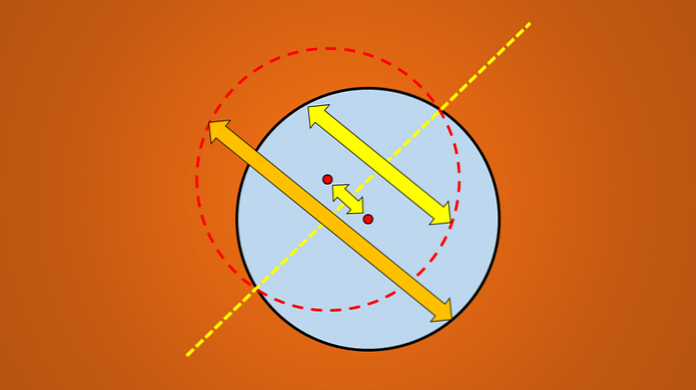
אבל אם התמונה הבאה נחשבת, זה ידוע היטב כי הקו נמשך הוא ציר של סימטריה של המעגל.

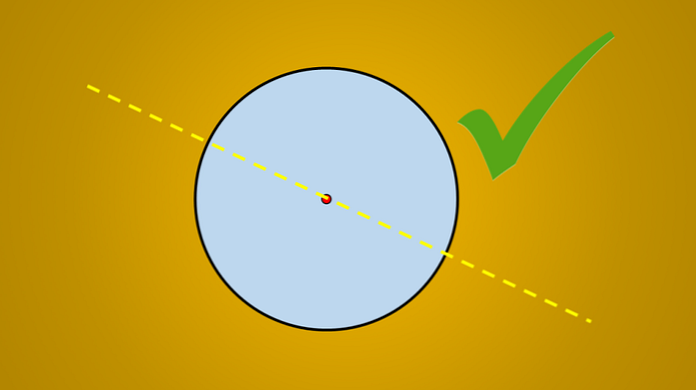
השאלה היא: האם יש עוד צירים של סימטריה? התשובה היא כן. אם אתה מסובב את הקו הזה 45 ° נגד כיוון השעון, הקו המתקבל הוא גם ציר של סימטריה של המעגל.

אותו הדבר קורה אם אתה מסובב 90 °, 30 °, 8 °, ובאופן כללי, כל מספר מעלות.

הדבר החשוב בקווים האלה הוא לא הנטייה שיש להם, אבל כולם עוברים במרכז המעגל. לכן, כל קו שמכיל קוטר של המעגל הוא ציר של סימטריה.

אז, מאז מעגל יש מספר אינסופי של קטרים, אז יש לה מספר אינסופי של צירים של סימטריה.

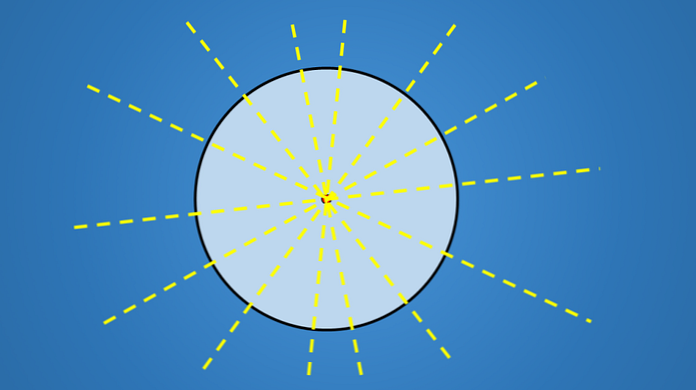
דמויות גיאומטריות אחרות, כגון משולש, מרובע, מחומש, משושה או כל מצולע אחר, יש מספר סופי של צירי סימטריה.

הסיבה למעגל יש מספר אינסופי של צירים של סימטריה היא שאין לה צד.

הפניות

1. באסטו, י 'ר. (2014). מתמטיקה 3: גיאומטריה אנליטית בסיסית. קבוצת העריכה של פטריה.
2. Billstein, R., Libeskind, S., & Lott, J. W. (2013). מתמטיקה: גישה לפתרון בעיות למורים לחינוך בסיסי. López Mateos עורכים.
3. Bult, B., & Hobbs, D. (2001). לקסיקון מתמטי (מאויר). (פ 'קדנה, טראד) מהדורות אקל.
4. Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). מתמטיקה גיאומטריה רפורמה של המחזור העליון של E.G.B. משרד החינוך.
5. שניידר, וו ', סאפרט, ד' (1990). שימושי טכני ציור ידני: מבוא את היסודות של ציור טכני תעשייתי. רוברט.
6. תומאס, ג 'ב', & וייר, ד '(2006). חישוב: מספר משתנים. חינוך פירסון.